I’m excited in this edition to present a podcast I recorded with Anastasis Makarieva about her work in developing the biotic pump theory, a theory that has gotten a lot of attention in recent years for articulating how forests can bring the rain. The theory describes how forest-evapotranspired water vapor condenses to create a pressure drop that sucks in moisture winds from the ocean.
Anastasia Makarieva was working towards her PhD in atmospheric physics in St Petersburg University, when she met physicist Victor Gorshkov. He was doing ground breaking research into how biology modulated the climate and environment to create conditions that support life better. She chose him to become her mentor, and together over the next two and a half decades they would develop a number of theories that furthered this paradigm.
In the West in the 1970s, James Lovelock, had been proposing that the earth has a self-regulating feedback loop that helps life create and maintain its own conditions for life. When Lovelock was asked by NASA to look for life on other planets, he came up with the perceptive observation that you could tell of the existence of life by whether the atmosphere was in equilibrium or or not. On earth, gases like oxygen, carbon dioxide, and nitrogen are in nonequilibrium. Geology alone could not create the concentrations of those gases. Microbes, plants, and animals are required. Lovelock proposed that life created the atmospheric composition percentages that was more favorable for life. Lovelock called his idea of a living, self-regulating earth, Gaia.
In the East, Victor Gorshkov, who had not heard of Lovelock’s work, was independently working along similar lines. He was working on a systems view of life and earth where climatology, evolutionary biology and genetics were not separate fields. Life evolved climate, and climate evolved life.
As Makarieva joined forces with Gorshkov, one of the questions they focused on was the curious nonequilibrium state of water on earth. On other planets, water reached a stationary equilibrium state. For example, on Venus as the planet got hotter, more water evaporated into the air. More water in the air, meant more heating, because water is a greenhouse gas. More heating meant more water evaporating, and so Venus gave rise to a runaway feedback loop until the planet go so hot, that all the water escaped to space. On Mars, it is so cold, that all the water exists in a steady state of ice, never melting. But on earth the water is nonstationary - water vapor will rise, condense, fall as rain, and then rise again. Makarieva and Gorshkov proposed life was helping keep water in this nonequilibrium state on earth. They wrote “Environmental parameters that are favourable for life on Earth are physically unstable. The liquid state of terrestrial hydrosphere, a major prerequisite for functioning of the contemporary living systems, is unstable with respect to spontaneous transition to either complete glaciation of the planetary surface or complete evaporation of the oceans. Without the stabilising biotic impact the environment and climate of Earth would rapidly degrade to a state prohibiting human existence.”
Makarieva and Gorshkov wondered if life was helping to bring rain onto the continents. They asked “if organisms can evolve ways to pump oxygen to their body with lungs, is it not also possible that the ecosystem can evolve ways to pump water to where its needed?”
They looked at the precipitation data around the globe. Where there were no forests around, rain drops exponentially as it moves inland. Where forests were around, for example, in the bioregions that contain the Amazon rainforests, the Congo rainforests, and the boreal forests of Russia, the amount of rain does not drop as it moves inland. Makarieva and Gorshkov figured the forests were attracting the rain.
The Biotic Pump
The mechanism they proposed for how forests attracted rain involved the high amount of water vapor evapotranspired by the forests. After rising into the atmosphere, water vapor condenses, leaving a partial vacuum (other gases are still present) where it once was. Water vapor takes up 2000 times the room liquid water does. The pressure drop created sucks in water moisture containing wind from the ocean.
Pressure drops can be quite powerful. Here’s an experiment you can do at home to demonstrate this. Fill a bottle with boiling water, then pour the water all out. Stick a straw in it with a sealant for the bottle. Hot water vapor is trapped in the bottle. Turn the bottle over, with the straw sticking into a bowl of water. The hot water vapor inside the bottle cools, which lowers the pressure inside the bottle. The water in the bowl then gets sucked up through the straw into the upside down bottle. Here is a Youtube video illustrating this phenomena:
Another experiment to demonstrate the power of water vapor pressure dropping was done by BBC show Earth Lab in a TV segment they did on Newcommen steam engines (the thermodynamic work cycle of the atmospheric circulation loop as the ocean wind blows into land and then back out again may have a lot of similarity to the thermodynamic work cycle of a Newcommen steam engine). In these steam engines when the water vapor condenses it creates a partial vacuum. The show filled a steel oil drum with steam, and then cooled the steam. The oil drum imploded dramatically (scaring the hosts). Below is a picture of the before and after of the oil drum. There were many injuries in the early days of steam engine development.
Atmospheric Circulations
In an atmospheric circulation loop, water vapor evaporates from the ocean, blows inland, rises up to create clouds, and then flows back out to sea.
The conventional meteorology story for what drives this atmospheric circulation is that the land is hotter than the ocean so air will rise, creating a place of lower pressure which then sucks the winds in. Here for example is a diagram from introductory teaching materials.
Makarieva and Gorshkov agreed with the basics of this story, but said there was a lot more to it - that it was also important to take into the partial vacuum force created by the condensing water vapor. The pressure drop induced was key in understanding the atmospheric circulation.
The biotic pump theory was published in a number of refereed journals. It sometimes was referred to by name as condensation induced atmospheric dynamics. Some of the later papers were published in collaboration with scientists from other universities - Andre Nobre, Ba-Lian Li, Douglas Sheil, Andrei Nefiokov, and Peter Bunyard.
As the biotic-pump/condensation-induced-atmospheric-dynamics theory became more well known, some critics argued that the latent heat released by the water vapor condensing would be an even larger effect than the pressure drop from the water vapor condensing. The biotic pump may happen, but it’s a small effect compared to the laten heat effect, they said.
Latent heat is the heat given off when water vapor turns to liquid. When thunderstorms begin, you can see a cumulus cloud get taller and taller. Introductory meteorology courses teaches that this is because there is so much water moisture releasing heat when they condense that the air currents start rising up, and the cloud gets taller. A thunderstorm cloud can rise as high as 6km. So latent heat is a significant effect. (The pressure drop might also play a role here in the cloud rise, something that conventional meteorology doesn’t mention.)
Makarieva and Gorshkov agree that the latent heat effect is bigger than the pressure drop in isolated systems, but they argue that when you take into account the whole atmospheric loop, then the pressure drop becomes more important than the latent heat. This is because the more heat that is added to air, the longer it will take for the air to cool down so it can sink again on. So latent heat increases the speed on the upward part of the atmospheric loop, but it decreases the speed on the downpart of the atmospheric loop. The latent heat is thus not very efficient at driving the whole atmospheric cycle.
I’ve been playing around with a number of ways to try and give an intuitive picture for the biotic pump and condensation induced atmospheric dynamics, to give an idea of the feasability of its physics, and also to shed light how it compares to the latent heat and land heating arguments of conventional meteorology.
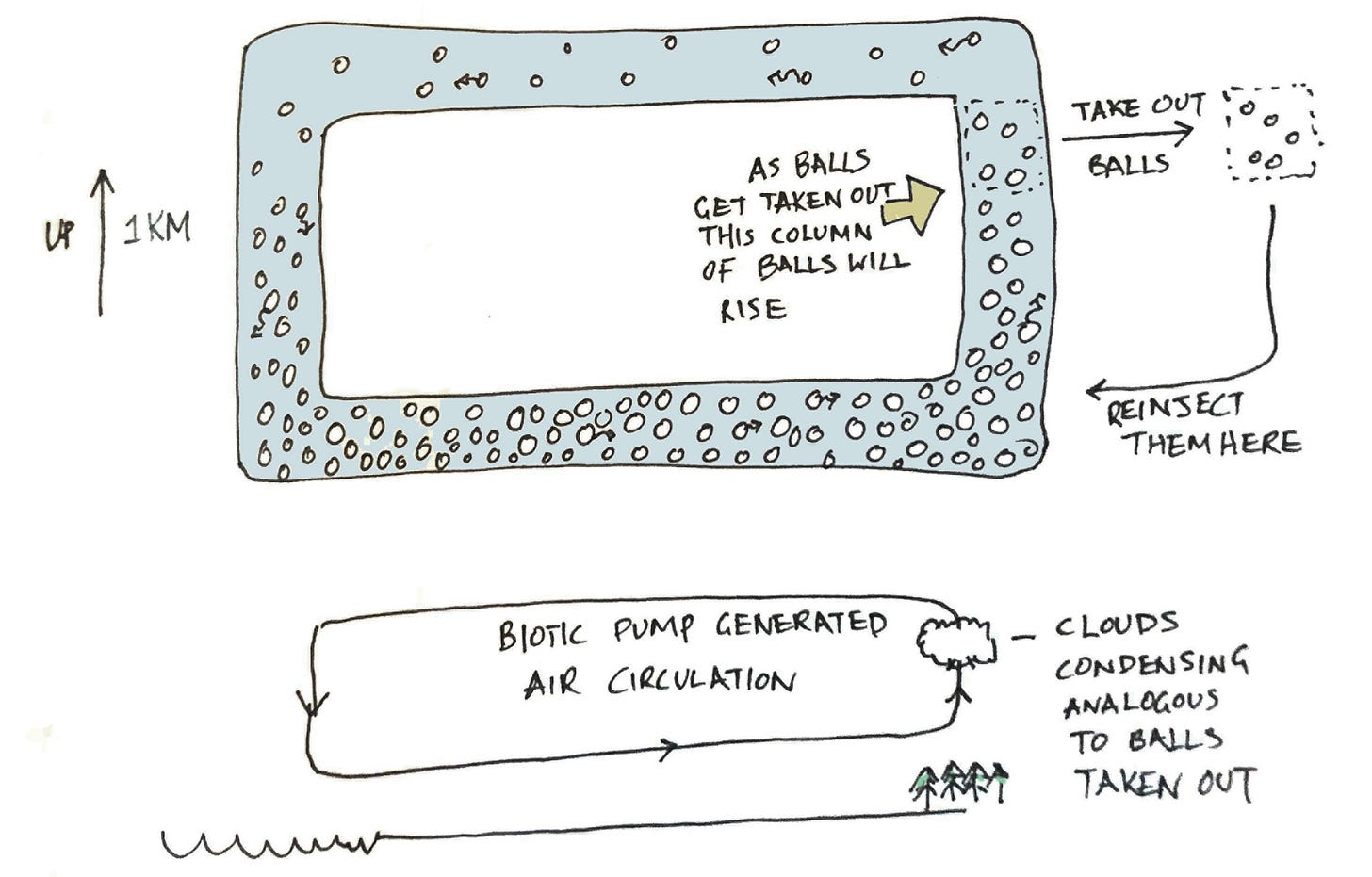
Here is a toy model that I think captures a lot of the relevant physics. Imagine a big pipe that forms a rectangular loop that rises up in the air vertically for a kilometer. The pipe is filled with bouncing balls. As you go up the number of balls gets less dense because of gravity. Initially there is no net circulatory movement of the balls. Then we take out a bunch of balls on the upper end of one of the sides of the loop. We then reinsert these balls at the bottom of that side. Because there are more balls below it, balls from below will stream upwards, thus initiating a movement of the balls around the whole loop. (See drawing below.) This is analogous to the act of water vapor condensing into a cloud and causing air atoms below to rise to fill it. The reinserting of the balls is analogous to rain falling down to be available to evapotranspire back up.
In general when a vacuum is created, there will be balls coming in to replace it from all directions. But since there are more balls bouncing around below, then there will be more pressure from below. By analogy, imagine piling books on top of each other up into the atmosphere. A ten thousand book pile will reach up to a kilometer. The books at the bottom will have a higher pressure, as the books above it are pushing down on it. This is what is called hydrostatic equilibrium. Now imagine that there is a spring also placed between each book. The compression of the spring gives an indication of the pressure. Now lets say we suddenly remove five hundred books from the top of the kilometer high pile. This creates a state called hydrostatic nonequilibrium, and the rest of the books push upwards and rise. In a similar way, when we remove balls from the right hand side of the Biotic Rectangle, it creates hydrostatic nonequilibrium, and many bouncing balls from below (including the balls that are reinserted) move upwards.
Now imagine if instead of taking the balls out where the dotted box says, we gave the balls in the dotted box more energy. This would be analogous to the latent heat release of the water vapor as it condenses into clouds. The balls there would then have a net movement up, and it would also drive some circulatory motion. However if we give the balls a lot of energy, they will not find it so easy to go down on the left land leg, and so the extra energy does not necessarily speed up the atmospheric motion through the whole loop. This is analogous to the Makarieva and Gorshkov argument for why latent heat is not so important for driving the atmospheric circulation.
In science, toy models can be very useful in demonstrating concepts and for calculating key behaviors. The Lotka Voltera model was as a simple of predator prey relationships that allowed some basic calculations of nonintuitive effects that occured in the wild. The radiative model of earth heating models the earth and its atmosphere as a one dimensional system, but it can give good approximations to the temperature on earth. The Biotic Rectangle may be a useful toy model to do some simple calculations on.
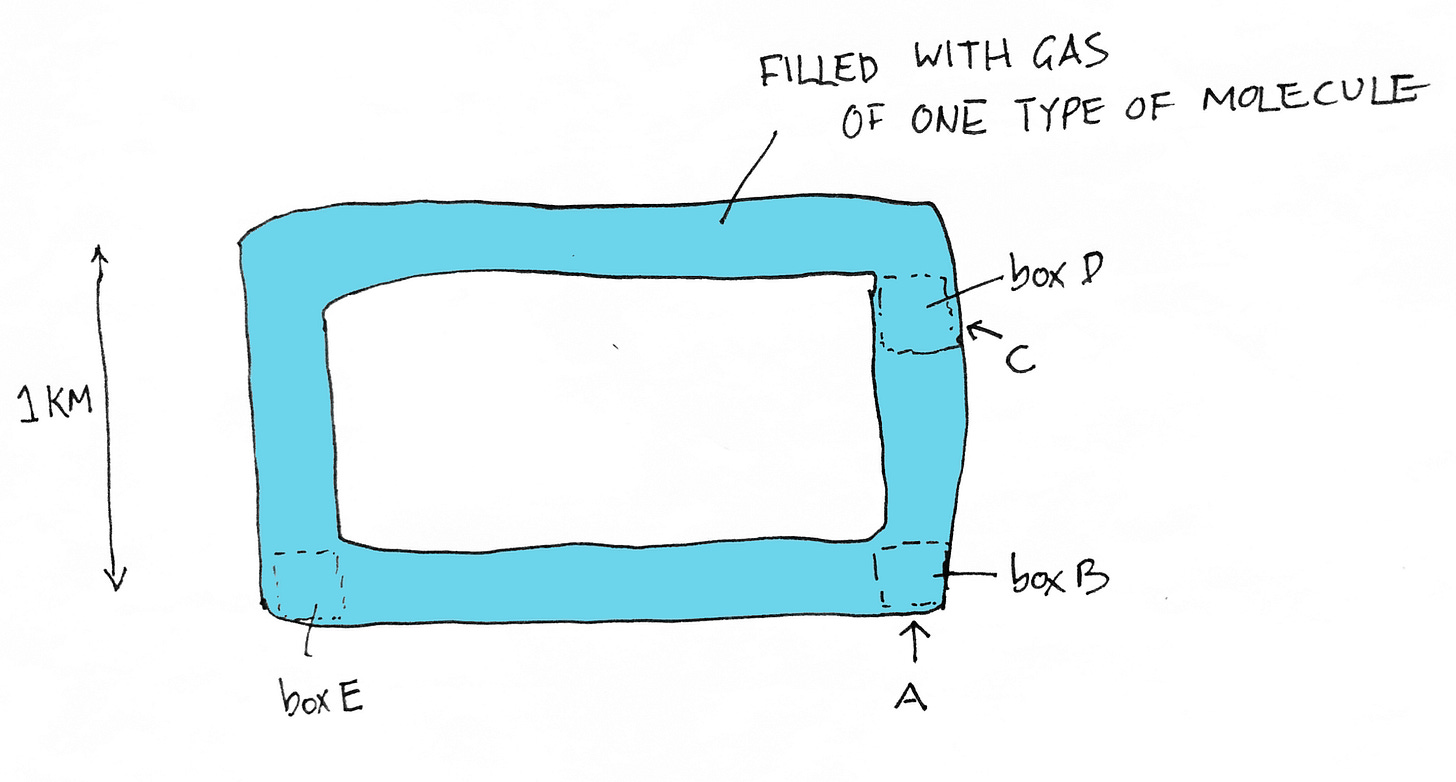
Instead of bouncing balls, lets imagine the rectangular pipe filled with an ideal gas made up of one type of molecule. At the top section of the pipe we can allow the taking out of heat from the system. This is analogous to the air radiating heat into space when it is in the top leg of the atmospheric loop. The gas cannot condense into a liquid. It is initially stationary.
What happens if we heat up the rectangle at position A? Will this cause the gas to start circulating, and if so at what velocity will the gas circulate the pipe given a certain amount of heat Q? If the gas does circulate, this is analagous to the standard meteorological argument given for why air circulates. We can ask what happens if we heat up the rectangle at point C. This is analogous to heat increasing (from latent heat release) as water vapor condenses into clouds. If we take out gas in the box D to leave a temporary vacuum, will this cause the gas to circulate, and if so, how fast? We can also ask ask if we put back the gas we take out at D into either box C or box E, how much will this affect the circulation? Putting it back in at box C is analogous to saying the rain that falls evapotranspires back up in the small water cycle. Putting it back in at E, is taking into account that there is input of water vapor from the ocean.
I think we can do some calculations based on this to determine the relative importance of standard meteorological factors compared to the biotic pump factor in generating atmospheric circulation. Feel free to pass this to amateur or professional physicists and atmospheric scientists to try their hand at calculating out this toy model. (There is share button at end of this article). And feel free to try it out yourself. Or if you want to collaborate on this problem with me, reach out. Either way, lets look together at the answers we get. And compare to the methods Makarieva and Gorshkov use.
What this model does is simplify the actual physical situation. In the atmospheric sciences, there is a fundamental set of equations that are called Primitive Equations used to model the movement of air in the atmosphere. The set includes the thermodynamics and the fluid dynamics (air for intensive purposes behaves like a liquid) equations that describe the movement of the air. These equations are used a lot to calculate many meteorological phenomena. However the problem is they don’t take into account that water can shift phases, that it will shift from vapor to liquid, and from liquid to vapor. They don’t take into account the temperature and pressures of these phase shifts. Those effects have to be tacked on, in not as elegant ways, with approximations of when to apply the Clausius-Clayperon equation (the equation that determines the temperature and pressure of phase changes), and by approximating ways to input when vegetation and soil evapotranspires water into the air.
In this Biotic Rectangle model we remove some of the complexities of these phase changes, and just simply say we take out the gas at a certain sink point, and put it back in at a certain source point. Then the model more closely resembles something that can be analysed by the Primitive Equations. Except for the vacuum created when we take out some of the gas. That part we have to figure out if we can model with normal reversible thermodynamics, or if we need to use more nonlinear equations like those for shock waves.
This model can be varied, as toy models can be, to make it simulate different aspects of reality. You can add more upward pipes to the rectangle to simulate that air can rise in multiple places on the land. You can add friction to the lower pipe to simulate how trees slow the flow of wind.
The Timing of the Forest Evapotranspiration
I asked Makarieva about whether lakes are also key to bringing in the rain, since they also evapotranspire. She replied that forests are more important, because they can control when they evapotranspire. If trees begin evapotranspiring as the humidity levels are rising (during the transition from dry to wet season), then the water vapor released helps push the humidity over the saturation point. The water vapor condensing then creates a pressure drop that sucks in the sea breeze. Its the timing that matters.
Imagine someone sitting on a swing. To make them go higher you want to push them at certain points in the swing. You want to push when the humidity is rising to a point where it can more easily go over the saturation point with some help from evapotranspiration. Forests may have evolved, or maybe learned when to push on the swing. Lakes on the other hand cannot control when they push on the swing.
In the Amazon, scientists looked at the isotopes of water in the rain at the onset of wet season, and found that it contained isotopes that come from the forest. It may be thats forests help initate the wet season.
I asked Makarieva about the climate simulations of Francina Dominguez (who we had previously interviewed here) who showed that forests slow the wind, thus helping to create rain. I thought maybe they were making different arguments. One was saying forests create wind, the other saying forests are slowing wind. Makarieva clarified that Dominguez’s theory is compatible with the biotic pump theory, as the condensation attracts the wind, and then the forests can slow the wind down when it arrives so it can create rain.
Large scale atmospheric circulations, extreme weather and hurricanes
The biotic pump effect also applies to large scale atmospheric circulatory systems like the Hadley Cell, the Ferrel Cell and the Walker cell (see this previous article in this newsletter) because they involve water condensation. These cells affect extreme weather events all over the world. The biotic pump affect applies to how hurricanes are generated. According to Makarieva and Gorshov calculations using the biotic pump give more more accurate values for wind velocity for hurricanes and for large scale circulations cells than do calculations made using standard meteorology. This is important because it can help us quantify how deforestration and afforestration affects extreme weather events. More on this in upcoming newsletter editions.
…………………….
I recorded this podcast several months ago, but because I wanted to understand the biotic pump effect more before I wrote about it, I have since spent a lot of time reading the research papers, trying to understand the math and physics, learning all the technical terms, and also giving myself an accelerated course in standard atmospheric science. I also spent a bit of time playing around with and developing intuitive models to capture the essense of the mathematics.
……………………..
This is a reader supported publication, and you are welcome, if you feel called, to financially support the research, recording and writing of this newsletter/podcast. This helps me spend more time working on this.
Appendix
Makarieva and Gorshkov in their paper Biotic pump of atmospheric moisture as driver of the hydrological cycle on land wrote “vaporation and transpiration cause an elevated moisture content in the vertical column of air over a forest, which, in turn, produces elevated condensation well above the canopy owing to the adiabatic ascent of moist air. The loss of gas out of the air column from condensation decreases air pressure well above the canopy, causing an increased vertical pressure gradient that results in an ascending air.” And “The non-equilibrium vertical distribution of atmospheric water vapor associated with the observed vertical lapse rate of air temperature produces an upward directed force, termed evaporative force, which causes the ascending motion of air masses, as well as the horizontal air motions from areas with low evaporation to areas with high evaporation.” [ref 1]
Makarieva and Gorschkov wrote in their paper The Biotic Pump: Condensation, atmospheric dynamics and climate that given a state where water moisture in air is above saturation - “such a hypothetical static distribution of vertically isothermal moist air is unstable. Any random upward displacement of an air volume leads to adiabatic cooling of the rising air. Air temperature drops such that the equilibrium partial pressure of water vapour dictated by the Boltzmann distribution becomes oversaturated at all heights where the moist saturated air ascends. This causes the water vapour to condense. Its partial pressure decreases down to the saturated pressure. Condensation diminishes the total air pressure and disturbs the hydrostatic distribution of moist air. The vertical gradient of air pressure becomes greater than the weight of a unit air volume. There appears an upward directed force acting on a unit air volume. A static equilibrium of moist air in the gravitational field is not possible. The air begins to ascend along the non-equilibrium pressure gradient produced by condensation. Condensation is sustained by continuous evaporation of water vapour from the hydrosphere. The upward-directed force that acts on moist air and causes it to rise adiabatically is termed the evaporative-condensational force (Makarieva and Gorshkov, 2007, 2009a).
Importantly, the evaporative-condensational force causes air to ascend adiabatically,
i.e., with no exchange of heat, over a large area with linear size exceeding the vertical
scale height h even if the atmosphere is initially vertically isothermal. This is not a
buoyancy-related force traditionally invoked to explain convective instability.
In a vertically isothermal atmosphere, a small air parcel with linear dimensions
smaller than h may occasionally ascend due to the Archimedes force − if temperature
fluctuations make the parcel warmer than the surrounding air. But, as the air parcel cools while ascending, its positive buoyancy disappears and the motion extinguishes
Moreover, the mixing of such parcels with surrounding air destroys the adiabatic
character of their motion. Most condensed water vapour leaves the atmosphere as precipitation. A minor part is maintained in the atmosphere by the rising air flow. This imposes a drag force on rising air and reduces its vertical velocity. In Section 6, we discuss the significance of this gravitational drag for condensation-induced air motions. Unlike the flow of water vapour, which condenses while rising, the flow of dry air components, which conserve their mass, cannot be unidirectional (vertical), because the dry air does not disappear as it ascends. For this reason, regions of horizontal air flow will appear. Condensation of water vapour in the ascending air produces both vertical and horizontal pressure gradients. The presence of water vapour in the atmosphere contacting with a liquid hydrosphere leads to the formation of three-dimensional circulation patterns. To this point in time, these complex condensation-induced air motions have not received consideration from
meteorologists.” [ref 2]
References
A. M. Makarieva, V. G. Gorshkov. Biotic pump of atmospheric moisture as driver of the hydrological cycle on land. Hydrology and Earth System Sciences Discussions, 2006, 3 (4), pp.2621-2673. https://hal.science/hal-00298762
Makarieva A.M., Gorshkov V.G. (2010) The Biotic Pump: Condensation, atmospheric dynamics and climate. International Journal of Water, 5(4), 365-385.

















Share this post